Η πληροφορία δεν είναι μια έννοια καθαρά μαθηματική. Αντίθετα μάλιστα, πάντα έχει μια σχέση με τον φυσικό κόσμο. Στην παραδοσιακή επιστήμη της πληροφορίας η σχέση της με τον φυσικό κόσμο ακολουθεί την κλασσική, μη κβαντική φυσική. Η κβαντική πληροφορική επιστήμη αντίθετα, είναι εκείνη που συνδέει την πληροφορία με την κβαντική θεωρία.

Η μετάδοση της κλασσικής πληροφορίας γίνεται με το bit, το οποίο είναι πάντα 0 ή 1. Η κβαντική πληροφορία μεταδίδεται με κβαντικά bits ή qubits.

Τι είναι όμως τα qubits; 

Ένα bit μπορεί να έχει μια εκ των δύο καταστάσεων : 0 ή 1. Ένα bit μπορεί να παρασταθεί με ένα τρανζίστορ το οποίο θα βρίσκεται είτε στην κατάσταση "on" που θα άγει, είτε στην κατάσταση "off" που δεν θα άγει. Μπορεί επίσης να παρασταθεί με ένα βέλος προς τα πάνω για την τιμή "1", είτε μ' ένα βέλος προς τα κάτω για την τιμή "0". 

Ας υποθέσουμε ότι οι δύο αυτές καταστάσεις του βέλους εκφράζουν τις δύο βασικές καταστάσεις ενός κβαντικού φυσικού μεγέθους όπως πχ το σπιν ενός ηλεκτρονίου, που είναι γνωστό ότι για κάθε συγκεκριμένο άξονα στον χώρο, μπορεί να πάρει μόνο τις τιμές +1/2 ή -1/2. Το +1/2 αντιστοιχεί στο βέλος προς τα επάνω και το -1/2 στο βέλος προς τα κάτω. Ας παραστήσουμε λοιπόν τις δύο βασικές καταστάσεις του σπιν του ηλεκτρονίου ως |↑> και ê↓> αντίστοιχα. Όπως όμως διδάσκει η κβαντομηχανική, ένα ηλεκτρόνιο μπορεί να βρεθεί σε μια γραμμική επαλληλία των δύο αυτών βασικών καταστάσεων:          ½â ñ =  w ê↑> + z ê↓>.

Μια τέτοια γραμμική επαλληλία εκφράζει φυσικά τον προσανατολισμό του σπιν του ηλεκτρονίου προς μια τυχαία κατεύθυνση στο χώρο. Η υπέρθεση αυτή των βασικών καταστάσεων, η οποία είναι το qubit, μπορεί να μεταφέρει πολλές πληροφορίες (θεωρητικά άπειρες), αφού οι συνδυασμοί των συντελεστών w και z δεν έχουν περιορισμό.
Η απεικόνιση των bits και των qubits με βέλη που παριστάνουν κβαντικές καταστάσεις του σπιν δείχνονται σχηματικά στην παρακάτω εικόνα:

Στην εικόνα αυτή δείχνεται το qubit σαν ένα βέλος του σπιν που καταλήγει σε μια οποιαδήποτε τοποθεσία, στην επιφάνεια μιας σφαίρας. Στη σφαίρα αυτή ο βόρειος πόλος είναι ισοδύναμος με σπιν +1/2 ή αλλιώς με την τιμή 1 του qubit, ενώ ο νότιος πόλος είναι ισοδύναμος με σπιν –1/2 ή με την τιμή 0 του qubit. Οι άλλες τοποθεσίες της σφαίρας είναι οι κβαντικές υπερθέσεις των καταστάσεων του σπιν ê↑>  και ê↓> ή αλλιώς του 1 και του 0. Η σφαίρα αυτή που λέγεται σφαίρα του Riemann και η στερεογραφική προβολή των διαφόρων σημείων της σ' ένα μιγαδικό επίπεδο που περνάει από τον ισημερινό της σφαίρας, παίζει μεγάλο ρόλο στην άλγεβρα των qubits και γενικότερα στο λογισμό που σχετίζεται με φυσικά συστήματα τα οποία έχουν δύο μόνο βασικές καταστάσεις. Μας βοηθάει όπως λέμε στην αναπαράσταση των χώρων Hilbert δύο διαστάσεων. Κάτι τέτοιο όμως ξεφεύγει από τα πλαίσια του παρόντος άρθρου και θα αποτελέσει αντικείμενο ενός άλλου άρθρου με θέμα τον λογισμό γύρω από το σπιν των ηλεκτρονίων.

Λέμε ότι το qubit περιέχει δυνητικά άπειρη πληροφορία, διότι οι συντελεστές  w και z στην υπέρθεση των βασικών καταστάσεων εξαρτώνται ουσιαστικά από τις συντεταγμένες του σημείου επί της σφαίρας που εκφράζει το qubit. Συνεπώς μπορεί να περιέχουν κατ’ αρχήν, άπειρη αλληλουχία ψηφίων, όπως δηλώνεται στο παραπάνω σχήμα με τη χρήση συντεταγμένων γεωγραφικού πλάτους και μήκους.

Η πληροφορία όμως ενός qubit πρέπει να εξαχθεί από αυτό κάποτε και κάτι τέτοιο γίνεται εκτελώντας μια μέτρηση. Στο παράδειγμά μας η μέτρηση αυτή είναι η μέτρηση του σπιν του ηλεκτρονίου σε κάποιον άξονα (πχ στον κατακόρυφο άξονα z ). Η κβαντομηχανική και πάλι μας λέει ότι κατά την μέτρηση, το αποτέλεσμα θα είναι πάντα μια από τις βασικές καταστάσεις: 0 ή 1. Η πιθανότητα όμως για το καθένα από αυτά τα αποτελέσματα μέτρησης εξαρτάται το «γεωγραφικό πλάτος» του βέλους. Αν το βέλος καταλήγει στο βόρειο ημισφαίριο θα έχουμε μεγαλύτερη πιθανότητα να πάρουμε ως αποτέλεσμα της μέτρησης «1». Αν καταλήγει στο νότιο τότε πιο πιθανό είναι να μετρήσουμε «0».

Στα πλαίσια της κβαντομηχανικής όταν καταπιανόμαστε με το πρόβλημα της φυσικής πραγματικότητας πρέπει να διακρίνουμε το «μετρήσιμο» από το «αντικειμενικό». Είναι αλήθεια ότι το διάνυσμα καταστάσεως του σπιν που είναι αποτέλεσμα υπέρθεσης δεν είναι μετρήσιμο, με την έννοια ότι δεν μπορούμε να διαπιστώσουμε πειραματικά τον ακριβή προσανατολισμό του σπιν. Όμως αυτή η υπέρθεση δείχνει να είναι μια καθαρά αντικειμενική ιδιότητα του ηλεκτρονίου αφού χαρακτηρίζεται πλήρως από τη στατιστική κατανομή των πειραματικών αποτελεσμάτων μέτρησης που παίρνουμε αν εκτελέσουμε πολλές φορές τη μέτρηση της ίδιας κατάστασης.

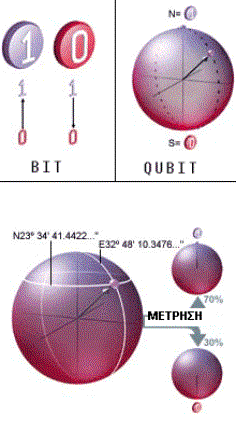
Στο παράδειγμα της εικόνας αν μετρήσουμε πολλές φορές τη ίδια κατάσταση σπιν που έχουμε προετοιμάσει προσεκτικά και λάβουμε ως στατιστικό αποτέλεσμα 70% και 30% , είμαστε σίγουροι ότι το σπιν είχε τον συγκεκριμένο προσανατολισμό με κατάληξη στο σημείο της σφαίρας που δείχνει το βέλος της εικόνας.