Το Θεώρημα Bell και η σημασία του για την πιθανοκρατική ερμηνεία της Κβαντομηχανικής  

Άρθρο, Δεκέμβριος 2002

Πολλές φορές έχει υποστηριχτεί ότι η τυχαιότητα και η πιθανοκρατία που παρατηρούμε στα κβαντομηχανικά φαινόμενα οφείλονται στο ότι υπάρχουν κάποιες κρυμμένες μεταβλητές οι οποίες καθορίζουν την εξέλιξη των φαινομένων αλλά δεν τις γνωρίζουμε. Υποστηρίζουν δηλαδή οι οπαδοί της θεωρίας των κρυμμένων μεταβλητών πως αν γνωρίζαμε αυτές τις άγνωστες μεταβλητές των κβαντικών συστημάτων, τα κβαντικά φαινόμενα θα έμοιαζαν και αυτά ντετερμινιστικά και απολύτως προβλεπτά.

Το 1969 όμως ο S. Bell απέδειξε ότι καμιά θεωρία κρυμμένων μεταβλητών που διατηρεί τις παραδοχές της τοπικότητας και του ντετερμινισμού δεν μπορεί να πετύχει τις προβλέψεις της κβαντικής φυσικής.
Αυτό είναι ένα θεωρητικό πόρισμα ζωτικής σημασίας και γι αυτό κατά την τελευταία τριακονταετία αποτέλεσε την κύρια πηγή πολλών θεωρητικών και πειραματικών ερευνών.

Το Θεώρημα ή η ανισότητα του Bell

Θ' αρχίσουμε τη μελέτη μας του θεωρήματος του Bell, με κάποιες παρατηρήσεις γύρω από τυχαία γεγονότα. Ας πάρουμε ένα φύλο χαρτί και ας γράψουμε στη σειρά τρία σύμβολα που το καθένα τους μπορεί να είναι το + ή το - σε τυχαία σειρά. Κάτω από την πρώτη τριάδα γράφουμε πάλι μια νέα τυχαία τέτοια τριάδα, και επαναλαμβάνουμε το ίδιο πράγμα κάμποσες φορές. Ένα παράδειγμα αυτής της διαδικασίας δίνει ο πίνακας 1. Ας συμβολίσουμε τις τρεις στήλες με τα γράμματα h, φ και θ.

Το επόμενο βήμα είναι να μετρήσουμε σε πόσες σειρές κάτω από τις στήλες h και φ υπάρχει το + και να παραστήσουμε αυτό τον αριθμό με n(h = +, φ = +). Στο παράδειγμά μας είναι 3.
Τώρα μετράμε σε πόσες σειρές στη στήλη φ υπάρχει το - και στη θ το +, και αυτό τον αριθμό τον παριστάνουμε με n(φ = -, θ = +). Στο παράδειγμα του πίνακα είναι 5.
Τέλος βρίσκουμε τον n(h = +, θ = +). Στο παράδειγμά μας είναι 4.

Αν προσθέσουμε τους δύο πρώτους αριθμούς, και βέβαια εφόσον έχουμε εφαρμόσει σωστά τις οδηγίες, θα βρούμε ότι το άθροισμα είναι πάντα μεγαλύτερο ή ίσο από τον τρίτο αριθμό. Δηλαδή:

                                     n(h = +, φ = +) + n(φ = -, θ = +)  n(h = +, θ = +)        (Σχέση 1)

Αν νομίζετε ότι μπορείτε να βρείτε ένα σύνολο τριάδων από + και - που να μην υπακούει σ' αυτή τη σχέση, μπορείτε να ξαναδοκιμάσετε. Σίγουρα δεν θα το καταφέρετε γιατί είναι αδύνατον.

Είναι πολύ εύκολο να αποδείξουμε ότι η σχέση (1) ισχύει για όλα τα σύνολα του τύπου που περιγράψαμε.

Ας εξετάσουμε πρώτα τον αριθμό των σειρών που έχουν h = + και φ = +. Αυτές οι σειρές περιλαμβάνουν δύο είδη τριάδων: τις τριάδες με h = +, φ = + και θ = + και τις τριάδες με h = +, φ = + και θ = -.

Δηλαδή:
n(h = +, φ = +) = n(h = +, φ = +,θ = +) + n(h = +, φ = +, θ = -).   (Σχέση 2)

Με τον ίδιο τρόπο έχουμε:
n(φ = -, θ = +) = n(h = +, φ = -, θ = +) +  n(h = -, φ = -, θ = +)   (Σχέση 3)   και

n(h = +, θ = +) = n(h = +, φ = +, θ = +) + n(h = +, φ = -, θ = +).  (Σχέση 4)

Αν προσθέσουμε τις σχέσεις (2) και (3) βρίσκουμε:

n(h = +, φ = +) + n(φ = -, θ = +) = n(h = +, φ = +,θ = +) + n(h = +, φ = +, θ = -) + n(h = +, φ = -, θ=+)
+n(h = -, φ = -, θ = +).

Όμως ο πρώτος και ο τρίτος όρος στο δεξιό μέλος αυτής της εξίσωσης δίνουν άθροισμα τον αριθμό:
                                                                n(h = +, θ = +)
Έχουμε συνεπώς:

n(h = +, φ = +) + n(φ = -, θ = +) =  n(h = +, θ = +) + n(h = +, φ = +, θ = -) + n(h = -, φ = -, θ = +)≥ n(h = +, θ = +).

Αποδείξαμε δηλαδή την σχέση (1).

Μια γεωμετρική παραλλαγή της ίδιας απόδειξης δίνεται στην παρακάτω εικόνα (1).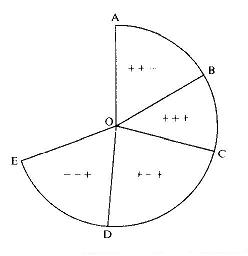

Επειδή AOC + COE ≥BOD θα έχουμε ότι: n(h = +, φ = +) + n(φ = -, θ = +) ≥n(h = +, θ = +)

Τι σχέση όμως έχουν όλα αυτά με τα πειράματα της κβαντομηχανικής; 

Πειράματα με πόλωση φωτονίων ελέγχουν την ισχύ του θεωρήματος

Φαντασθείτε τώρα ότι θα ήταν δυνατόν να μετρήσουμε την πόλωση ενός φωτονίου σε τρεις διαφορετικές κατευθύνσεις χωρίς να το διαταράξουμε καθόλου, και να βρούμε αν ήταν:

α) παράλληλη ή κάθετη στην οριζόντια διεύθυνση
β) παράλληλη ή κάθετη σε μια διεύθυνση υπό γωνία φ ως προς την οριζόντια και
γ) παράλληλη ή κάθετη σε μια διεύθυνση υπό γωνία θ ως προς την οριζόντια.

Αν σε κάθε περίπτωση γράψουμε (+) όταν η πόλωση είναι παράλληλη, και (-) όταν είναι κάθετη, και επαναλάβουμε αυτή την μέτρηση αρκετές φορές, θα πάρουμε ένα σύνολο τιμών, σαν αυτό που περιγράψαμε παραπάνω, που θα υπακούει στην σχέση (1).

Φυσικά αυτό το πείραμα δεν μπορούμε να το κάνουμε στην πράξη, γιατί ξέρουμε ότι είναι αδύνατο να πραγματοποιήσουμε ανεξάρτητες μετρήσεις για τις τρεις συνιστώσες πόλωσης ενός μοναδικού φωτονίου.

Μπορούμε όμως να χρησιμοποιήσουμε συσχετισμένα φωτόνια.

Ας δούμε λοιπόν σε συντομία τι είναι αυτά τα συσχετισμένα φωτόνια.

Ας θεωρήσουμε ένα φυσικό σύστημα αποτελούμενο από άτομα, στα οποία συμβαίνει μια μετάπτωση από μια διεγερμένη στάθμη στη θεμελιώδη , με τη διαδοχική εκπομπή δύο φωτονίων. Τα φωτόνια αυτά έχουν διαφορετικά μήκη κύματος, αντιστοιχούν δηλαδή σε διαφορετικά χρώματα. Η σημαντική όμως ιδιότητά τους είναι ότι οι πολώσεις τους είναι πάντα κάθετες μεταξύ τους. Αν πχ. το ένα είναι πολωμένο υπό γωνία +45^ο ως προς την οριζόντια διεύθυνση, το άλλο θα έχει πόλωση -45^ο κοκ. Φυσικά αυτή την ιδιότητα δεν την έχουν όλα τα άτομα που εκπέμπουν φωτόνια κατά ζεύγη, αλλά μερικά μόνο. Τέτοιου είδους φωτόνια ονομάζονται συσχετισμένα (entangled).

Αποδεικνύεται λοιπόν ότι όλες οι ποσότητες που περιέχονται στη σχέση (1), μπορεί να ληφθούν από μετρήσεις σε συσχετισμένα ζεύγη φωτονίων, με τον όρο ότι ισχύουν οι παραδοχές της θεωρίας των κρυμμένων μεταβλητών για την τοπικότητα και τον ντετερμινισμό: δηλαδή υπό τον όρο ότι η πόλωση ενός φωτονίου δεν επηρεάζεται από την μέτρηση του άλλου που βρίσκεται μακριά και ότι το αποτέλεσμα κάθε μέτρησης καθορίζεται από κάποια κρυμμένη ιδιότητα του φωτονίου.

Ας θεωρήσουμε τρία ξεχωριστά πειράματα με τις διατάξεις της εικόνας (2). Στο πρώτο, στα αριστερά μετρείται η πόλωση ΟΚ (Οριζόντια ή Κατακόρυφη) και στα δεξιά η πόλωση φ_±. Δεχόμενοι την τοπικότητα, μπορούμε να πούμε ότι κάθε φορά που ανιχνεύεται ένα φωτόνιο στην αριστερή κατακόρυφη οδό, στα δεξιά, αν υπήρχε όμοια συσκευή, θα ανιχνευόταν ένα φωτόνιο στην οριζόντια οδό. Απ' αυτό συμπεραίνουμε ότι αν επαναλαμβάναμε το πείραμα πολλές φορές, για τα δεξιά φωτόνια θα βρίσκαμε μια τιμή του αριθμού

n(ο= +, φ =+). Δηλαδή n(κ, φ₊) = n(o = +, φ = +).  (Σχέση 5)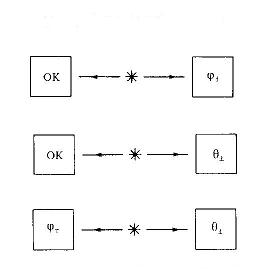

Ας θεωρήσουμε τώρα το δεύτερο πείραμα, όπου η δεξιά συσκευή επαναπροσανατολίζεται ώστε να κάνει μετρήσεις σε κάποια άλλη διεύθυνση (π.χ. υπό γωνία θ ως προς την οριζόντια) ενώ η αριστερή παραμένει στις ΟΚ. Με τον ίδιο ακριβώς τρόπο βρίσκουμε ότι: n(κ, θ₊⁾ = n(o = +,θ = +)    (Σχέση 6).  

Φυσικά δεν κάναμε τις μετρήσεις στα ίδια σύνολα ζευγών φωτονίων αλλά αν είχαμε πολλά ζεύγη, τον ίδιο αριθμό και στα δύο πειράματα, συμπεραίνουμε ότι αν η δεξιά συσκευή στο δεύτερο πείραμα είχε την διεύθυνση φ, τότε ο αριθμός n(κ, φ₊) θα ήταν ίδιος με πριν, εξαιρώντας τις μικρές στατιστικές διακυμάνσεις.)

Τέλος αν θεωρήσουμε το τρίτο πείραμα όπου η αριστερή συσκευή προσανατολίζεται στη διεύθυνση φ ενώ η δεξιά παραμένει στη διεύθυνση θ. Όπως πριν κάθε φορά που βρίσκουμε ένα αριστερό φωτόνιο στη οδό φ₊ δεχόμαστε ότι στα δεξιά το άλλο φωτόνιο θα βρίσκεται στην οδό φ_- . Συμπεραίνουμε λοιπόν ότι:

 n(φ₊, θ₊) = n(φ = -, θ = +)    (Σχέση 7).

Εφόσον λοιπόν είναι σωστές οι παραδοχές μας, από τις παραπάνω σχέσεις (1, 5, 6, 7) βρίσκουμε αμέσως ότι:

 n(κ, φ₊) + n(φ₊, θ₊) ≥ n(κ, θ₊⁾   (Σχέση 8).

Το θεώρημα ή αλλιώς ανισότητα του Bell, με λόγια εκφράζεται ως εξής: 

Αν εκτελέσουμε τρία πειράματα για να μετρήσουμε τις πολώσεις μεγάλου αριθμού ζυγών φωτονίων στα οποία ο αριστερός και ο δεξιός πολωτής είναι αντίστοιχα:
(α) κατακόρυφος και υπό γωνία φ ως προς την οριζόντια διεύθυνση,
(β): κατακόρυφος και υπό γωνία θ και
(γ): υπό γωνία φ ο αριστερός και θ ο δεξιός,
τότε ο συνολικός αριθμός των ζευγών του (β) πειράματος, όπου και τα δύο φωτόνια καταγράφονται θετικά, δεν μπορεί ποτέ να είναι μεγαλύτερος από το άθροισμα των ζευγών φωτονίων, όπου και τα δύο φωτόνια καταγράφονται θετικά στα πειράματα (α) και (γ).

Είναι βέβαια προϋπόθεση ότι πάντα τα αποτελέσματα των πειραμάτων καθορίζονται από κρυμμένες μεταβλητές που κατέχουν τα φωτόνια και ότι η κατάσταση κάθε φωτονίου δεν επηρεάζεται από τη μέτρηση της άλλης συσκευής, που βρίσκεται μακριά.

Και το συμπέρασμα των πειραμάτων;

Ας δούμε τώρα αν η κβαντική θεωρία συμβιβάζεται με την ανισότητα Bell. Η κβαντική τιμή του αριθμού 
n(κ, φ₊) είναι ανάλογη του τετραγώνου της συνιστώσας της έντασης του ηλεκτρικού πεδίου κατά τη διεύθυνση φ, όταν η ένταση έχει την οριζόντια διεύθυνση. Βλέπε (εικόνα 3).

(Εικόνα 3) Όταν  το αριστερό φωτόνιο είναι κατακόρυφα πολωμένο, το δεξιό είναι οριζόντια.Προβάλλουμε λοιπόν την ένταση του οριζόντιου ηλεκτρικού πεδίου στον άξονα φ, και παίρνουμε: Ε_φ+ = Εσυνφ. Επειδή στο τετράγωνο διότι ο αριθμός n(κ, φ₊) ουσιαστικά εκφράζει την ένταση Ι της ακτινοβολίας, που περνά από τον πολωτή, αυτή είναι ανάλογη του τετραγώνου της έντασης του πεδίου Ε_φ+. Ισχύει λοιπόν ότι  n(κ, φ₊) = Ν/2·συν²φ. Ν είναι ο συνολικός αριθμός των φωτονίων.

Για να βρούμε την τιμή του n(φ_+, θ_- ) παρατηρούμε ότι αν στρέψουμε τους άξονες κατά γωνία φ, η διεύθυνση φ₊ θα αντιστοιχεί στη νέα οριζόντια διεύθυνση, και η διεύθυνση θ₊ σχηματίζει με αυτήν γωνία (θ-φ). Τότε με όμοιο συλλογισμό όπως παραπάνω βρίσκουμε ότι: n(φ₊, θ₊) = Ν/2·ημ²(θ-φ).

Συνεπώς η κβαντική θεωρία θα είναι συμβιβαστή με την ανισότητα όταν και μόνον όταν για κάθε δυνατή τιμή των θ και φ ισχύει η σχέση:
                                            συν²φ + ημ²(θ-φ) ≥συν²θ   (Σχέση 9)

Αντίστροφα για να αποδείξουμε ότι η κβαντική θεωρία είναι ασυμβίβαστη με την ανισότητα Bell, αρκεί να δείξουμε ότι για ορισμένες τιμές των θ και φ η ανισότητα (9) δεν αληθεύει.

Μας βολεύει να εξετάσουμε την ειδική περίπτωση φ = 3θ. Η (εικόνα 3) παριστάνει γραφικά τη διαφορά των δύο μελών της σχέσης (9) σε συνάρτηση με τη θ.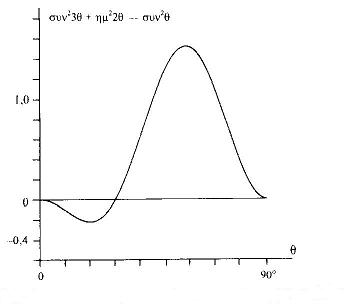

Σ ' αυτή την περίπτωση παρατηρούμε ότι  η ανισότητα Bell ισχύει για γωνίες θ μεγαλύτερες από 30^ο ενώ παραβιάζεται για γωνίες από 0^ο έως 30^ο . Αν δηλαδή η κβαντική φυσική ήταν συμβιβαστή με το θεώρημα του Bell η συνάρτηση συν²3θ + ημ²2θ - συν²θ έπρεπε να είναι θετική ή μηδέν για όλες τις τιμές της θ. Αυτό όμως δεν ισχύει όπως φαίνεται από το διάγραμμα για 0^ο < θ < 30^ο.

Οδηγούμαστε λοιπόν στο συμπέρασμα ότι είτε η κβαντική θεωρία δεν προβλέπει σωστά τα αποτελέσματα των μετρήσεων της πόλωσης των συζευγμένων φωτονίων, είτε είναι λαθεμένη κάποια από τις παραδοχές στις οποίες στηρίζεται το θεώρημα του Bell. Όμως οι παραδοχές αυτές είναι ότι το αποτέλεσμα του πειράματος μέτρησης ενός φωτονίου δεν επηρεάζεται από την παρουσία μιας άλλης μετρητικής συσκευής που βρίσκεται πολύ μακριά, και ακόμα ότι τα αποτελέσματα τέτοιων μετρήσεων καθορίζονται από κάποια εσωτερική ιδιότητα του φωτονίου την οποία εμείς απλώς αγνοούμε.

Περιττό βέβαια να πούμε ότι τα πειράματα που έγιναν όλα τα τελευταία χρόνια συμφωνούσαν με τις κβαντικές προβλέψεις και παραβίαζαν την ανισότητα Bell. Ένα από τα πιο αποφασιστικά πειράματα στον τομέα αυτό στάθηκε το πείραμα του Alain Aspect στη Γαλλία, το 1982.

Σήμερα πια είναι αναμφισβήτητο ότι η παραβίαση της ανισότητας του Bell σημαίνει ότι δεν μπορεί να ισχύει καμιά θεωρία κρυμμένων μεταβλητών που διατηρεί την τοπικότητα.

Τέλος πρέπει να αναφέρουμε ότι υπάρχουν σοβαρές τεχνικές δυσκολίες που εμπόδισαν την άμεση πειραματική επαλήθευση της ανισότητας Bell με τη μορφή που αναφέρθηκε στα παραπάνω. Οι δυσκολίες οφείλονταν κυρίως στο ότι ούτε οι πολωτές, ούτε οι ανιχνευτές φωτονίων έχουν απόδοση 100% οπότε δεν ανιχνεύονται όλα τα φωτόνια που εκπέμπει η πηγή. Γι αυτό ελέγχθηκε μια πιο περίπλοκη μορφή της ανισότητας Bell η οποία αναφέρεται σε πείραμα όπου οι μετρήσεις γίνονται με 4 διαφορετικούς προσανατολισμούς των πολωτών, αντί των 3 που εξετάσαμε παραπάνω.

Αναφορά

Το βιβλίο: "Quantum PhysicsQ; illusion or reality? του Alastair Rae (Εκδόσεις Cambridge University Press).