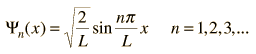|
A) Σωματίδιο σε φρέαρ (πηγάδι)
δυναμικού απείρου βάθους
 Μια
απλή περίπτωση στην οποία μπορεί να
χρησιμοποιηθεί η εξίσωση, είναι το
παρακάτω πρόβλημα ενός σωματιδίου σε
ένα πηγάδι δυναμικού απείρου βάθους
και πλάτους L. Μια
απλή περίπτωση στην οποία μπορεί να
χρησιμοποιηθεί η εξίσωση, είναι το
παρακάτω πρόβλημα ενός σωματιδίου σε
ένα πηγάδι δυναμικού απείρου βάθους
και πλάτους L.
Στο πηγάδι αυτό η δυναμική ενέργεια U(x)=0
στο διάστημα από 0<x<L ενώ
έξω από το πηγάδι (x < 0 ή x > L ) η
δυναμική ενέργεια U(x) είναι
άπειρη, άρα δεν μπορούν να υπάρξουν
εκεί σωματίδια.
Αυτό σημαίνει πως έξω από το πηγάδι η
κυματοσυνάρτηση Ψ(x) είναι
μηδέν, Ψ(x)=0.
Εντός του πηγαδιού όμως, λόγω
της τιμής της δυναμικής ενέργειας U(x)=0,
η εξίσωση του Schrödinger παίρνει τη
μορφή
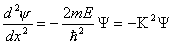 όπου
όπου 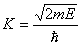
Η λύση της παραπάνω διαφορικής
εξίσωσης είναι της μορφής: Ψ(x)=Aημ(kx).
Οι οριακές συνθήκες που πρέπει να
ικανοποιεί η λύση αυτή είναι Ψ(0)=0
και Ψ(L)=0, αλλά για x=0
πράγματι η Ψ(x) =0.
Για να πάρουμε όμως Ψ(L)=0 θα
πρέπει το kx να είναι
kx=nπ. Βάζοντας στη σχέση αυτή τη
τιμή του K παίρνουμε:
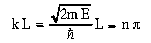
Από την οποία λύνοντας ως προς την
ενέργεια Ε παίρνουμε
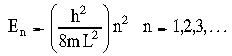 ή
ή
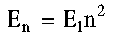 , ,
δηλαδή οι τιμές της ενέργειας
που μπορεί να πάρει ένα σωματίδιο είναι
κβαντισμένες σε αντίθεση με την
κλασσική φυσική. Επίσης βλέπουμε πως
επειδή n=1,2,3... η Ενέργεια Ε είναι
πάντα μη μηδενική. Αυτό συμφωνεί και με
την αρχή της αβεβαιότητας.
Αντικαθιστώντας επίσης την
σχέση k=nπ/x στην εξίσωση της
Ψ(x) οι επιτρεπτές κυματοσυναρτήσεις
είναι της μορφής:
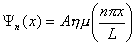
ή υπολογίζοντας την σταθερά Α με την
απαίτηση η συνολική πιθανότητα για το
διάστημα 0 έως L να ισούται με 1, τελικά
έχουμε:
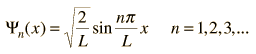
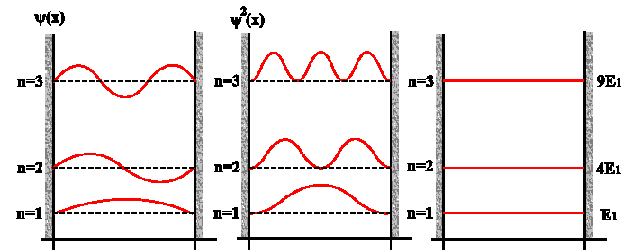
Στις παρακάτω εικόνες φαίνονται
οι κυματοσυναρτήσεις, οι πυκνότητες
πιθανότητας και οι ενεργειακές στάθμες
σε ένα πηγάδι απείρου βάθους:
Το φρέαρ αυτό δυναμικού με
άπειρα τοιχώματα χρησιμοποιείται για
την εύρεση των ενεργειακών σταθμών των
ηλεκτρονίων που περιφέρονται γύρω από
τον πυρήνα των ατόμων.
Μια άλλη εφαρμογή είναι και το
φρέαρ (πηγάδι) δυναμικού πεπερασμένου
βάθους που χρησιμοποιείται στην
περίπτωση των ελεύθερων ηλεκτρονίων
μέσα σε ένα μέταλλο ορισμένου πλάτους.
Β) Σωματίδιο σε πηγάδι (φρέαρ)
δυναμικού πεπερασμένου βάθους
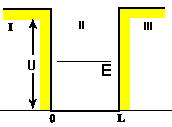 Έστω
ένα σωματίδιο με ενέργεια Ε εντός
ενός ορθογώνιου πηγαδιού δυναμικού με
πεπερασμένο βάθος U (που είναι η
δυναμική ενέργεια) και πλάτος x=L.
Θεωρούμε ότι το μηδενικό επίπεδο
της ενέργειας βρίσκεται στον πυθμένα
του πηγαδιού. Η κλασσική φυσική ορίζει
ότι αν η ενέργεια Ε του σωματίου είναι
μικρότερη από την δυναμική ενέργεια U,
τότε το σωματίδιο δεν μπορεί να φύγει
από το πηγάδι. Δηλαδή θα μείνει
κλεισμένο στην περιοχή ΙΙ (0<x<L)
για πάντα. Έστω
ένα σωματίδιο με ενέργεια Ε εντός
ενός ορθογώνιου πηγαδιού δυναμικού με
πεπερασμένο βάθος U (που είναι η
δυναμική ενέργεια) και πλάτος x=L.
Θεωρούμε ότι το μηδενικό επίπεδο
της ενέργειας βρίσκεται στον πυθμένα
του πηγαδιού. Η κλασσική φυσική ορίζει
ότι αν η ενέργεια Ε του σωματίου είναι
μικρότερη από την δυναμική ενέργεια U,
τότε το σωματίδιο δεν μπορεί να φύγει
από το πηγάδι. Δηλαδή θα μείνει
κλεισμένο στην περιοχή ΙΙ (0<x<L)
για πάντα.
Η κβαντομηχανική όμως λύση του
προβλήματος με τη βοήθεια της εξίσωσης
Schrödinger, ορίζει ότι η πιθανότητα να
βρεθεί το σωματίδιο εκτός του πηγαδιού
(περιοχή Ι και ΙΙΙ) είναι διάφορη του
μηδενός. Άρα είναι και η πυκνότητα
πιθανότητας, που δίνεται από το
τετράγωνο της κυματοσυνάρτησης Ψ2
.
Για τις περιοχές Ι και ΙΙΙ η
δυναμική ενέργεια ή δυναμικό U είναι
διάφορη του μηδενός ενώ στην περιοχή Ι
το δυναμικό είναι μηδέν.
Επίσης στις περιοχές Ι και ΙΙΙ η
εξίσωση του Schrödinger γίνεται, 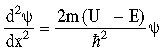
Αντικαθιστώντας με 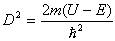 θα πάρουμε
θα πάρουμε 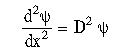 . .
Η συνθήκη κανονικοποίησης
επιβάλλει ότι για την περιοχή Ι (x<0) η
κυματοσυνάρτηση Ψ γίνεται : Ψι=ΑeDx
ενώ για την περιοχή ΙΙΙ η
κυματοσυνάρτηση Ψ γίνεται Ψιιι=Αe-Dx
δηλαδή μειώνονται εκθετικά
καθώς αυξάνεται απολύτως το x.
Όμως στην περιοχή ΙΙ η
κυματοσυνάρτηση είναι αρμονική, λόγω
του γεγονότος ότι U=0. Έτσι η
κυματοσυνάρτηση Ψιι
γίνεται: ΨΙΙ=Cημ(kx)+Eημ(kx)
, όπου 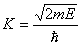 . .
|
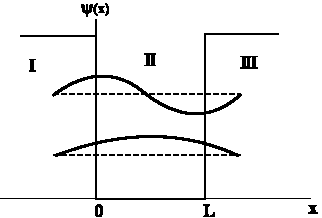
Κυματοσυναρτήσεις των δύο
χαμηλότερων ενεργειακών
καταστάσεων σωματιδίου για n=1 και n=2
σε πηγάδι δυναμικού πεπερασμένου
βάθους. (Πάνω αριστερό σχήμα)
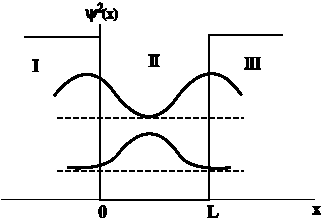
Στο κάτω αριστερό σχήμα
έχουμε τις πυκνότητες πιθανότητας
για τις δύο χαμηλότερες
ενεργειακές σωματιδίων σε πηγάδι
δυναμικού πεπερασμένου βάθους.
Να σημειωθεί πως οι
κυματοσυναρτήσεις είναι συνεχείς
στα όρια μεταξύ των τριών περιοχών,
όπως επίσης ότι δεν μηδενίζονται
στα τοιχώματα του πηγαδιού ούτε
έξω από αυτό.
Παρατηρούμε ότι αυτές
διεισδύουν και στις δύο
απαγορευμένες περιοχές (Ι και ΙΙΙ)
από την Κλασσική Φυσική. Επομένως η
πιθανότητα να βρούμε το σωματίδιο
έξω από το πηγάδι είναι μεγαλύτερη
του μηδενός.
Το γεγονός ότι η
κυματοσυνάρτηση Ψ είναι διάφορη
του μηδενός έξω από το πηγάδι
συνεπάγεται αύξηση του μήκους
κύματος de Broglie στην περιοχή ΙΙ,
πράγμα που σημαίνει μείωση της
ορμής και της ενέργειας του
σωματιδίου.
Όπως στο πρόβλημα πηγαδιού
απείρου βάθους έτσι κι εδώ οι
δυνατές ενέργειες του σωματιδίου
είναι κβαντισμένες.
Η εφαρμογή αυτή
χρησιμοποιείται στην περίπτωση
των ελεύθερων ηλεκτρονίων μέσα σε
ένα μέταλλο ορισμένου πλάτους.
|
Γ) Φαινόμενο σήραγγας
και εξίσωση Schrodinger
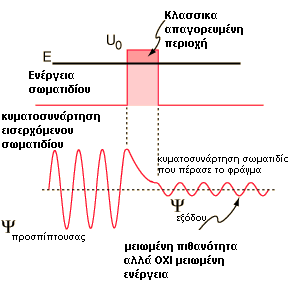 |
Σύμφωνα με την κλασσική
φυσική, ένα σωματίδιο ενέργειας E
μικρότερης από το ύψος U0 ενός
φράγματος δυναμικού δεν μπορεί να
διαπηδήσει (εισχωρήσει) στην
περιοχή του φράγματος. Αυτό
σημαίνει ότι η περιοχή στο άνω
εσωτερικό μέρος του φράγματος
είναι απαγορευμένη στην κλασσική
φυσική.
Όμως η κυματοσυνάρτηση που
συνδέεται με ένα ελεύθερο
σωματίδιο (μη υποκείμενο σε
δυνάμεις) πρέπει να συνεχίζεται
στο φράγμα και θα έχει μια εκθετική
μείωση στο εσωτερικό του φράγματος
δυναμικού. Η κυματοσυνάρτηση
πρέπει να είναι επίσης συνεχής
πέραν του φράγματος, έτσι υπάρχει
μια πεπερασμένη πιθανότητα ότι το
σωματίδιο θα ανοίξει σήραγγα μέσα
στο φράγμα και θα το διαπεράσει.
Στο φαινόμενο σήραγγας
οφείλεται η διάσπαση του πυρήνα
και η εκπομπή των σωματίων άλφα από
τους πυρήνες. Πρόκειται δηλαδή για
φαινόμενα όπου τα σωμάτια άλφα
έχουν μικρότερη ενέργεια από το
δυναμικό, και σύμφωνα με την
κλασσική φυσική δεν επιτρέπεται να
ξεφύγουν από τον πυρήνα. Η
κβαντομηχανική όμως με τη βοήθεια
της κυματοσυνάρτησης Ψ , μπορεί να
εξηγήσει θαυμάσια τι συμβαίνει
στον πυρήνα του ατόμου, και γιατί
τα σωμάτια α στην πραγματικότητα
διαφεύγουν.
Καθώς ένα σωματίδιο
προσεγγίζει το φράγμα,
περιγράφεται από μια
κυματοσυνάρτηση ελεύθερου (μη
δεσμευμένου) σωματιδίου. Όταν
φθάνει το φράγμα, πρέπει να
ικανοποιεί την εξίσωση του Schrödinger,
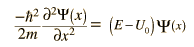
η οποία έχει εκεί έχει την
εξής λύση:
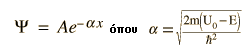
|
Αναφορές:
Κβαντομηχανική Berkeley, Στ. Τραχανά, Serway, Ο
κβαντικός κόσμος του J. C.
Polkinghorne, Το κβαντικό Σύμπαν των Tony Hey &
Patrick Walters καθώς και το βιβλίο της Γ!
Λυκείου Κόκκοτα, Περιστερόπουλου κλπ. |




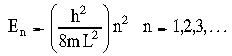 ή
ή